In the case of the previously treated inorganic compounds, we usually have to deal with solid substances in which the thermal energy is stored in the vibrations and translation and rotation practically do not play any role. In the case of the organic substances, translation, rotation and vibration are now present. In contrast to the inorganic substances, it is also the case that the thermodynamic data for organic compounds are related to significantly larger units. In the following section it is important to work out, that and how the storage of the thermal energy at translation and rotation levels is different from that of vibration.
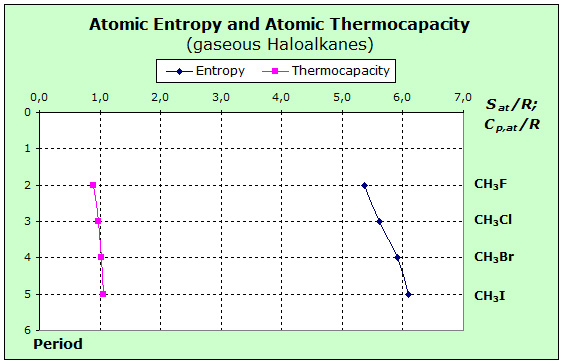
To begin with, we select monohalomethanes as an initial example. For these haloalkanes, the entropy values of the methane derivatives are shown in the following diagram:

Similar to the inorganic substances, it can be seen here that the variation in the thermal capacitance is less than in the entropy. Since we are dealing here with gaseous substances, it is close to a glance at the values of the noble gases. From the table in section 3.3, the entropy values are increased as the mass increases, while the thermal capacities remain constant. The particle mass obviously has a different effect on entropy and thermocapacity when comparing translational and vibrational states.

The Thermulation II program provides an overview of the fact that a larger mass only leads to greater storage capacity in the case of the vibration memories. Only in the larger entropy (due to the larger mass) is more thermal energy stored up to the same temperature. It is also found with this program that a constant contribution of 2.5 R to the translational portion of the thermal capacitance takes place when the translational entropy after ln(T) is derived. A constant contribution of 1.0 R is obtained for the rotation. As the mass increases, more and more thermal energy is stored with greater entropy, and when the vibrational entropy is derived after ln(T), the vibrational contribution to the thermal capacity increases. Since no real gas correction is carried out in the Thermulation II program, however, it must also be borne in mind that the deviation from the ideal gas will also affect the position of the energy levels.
With these background information, we can now look at and interpret the above diagram. In the case of the halomethane molecules in the gas state, the thermal energy can be stored both in translational, as well as in rotational and vibration states. For the entropy, therefore, these values will also rise in all three storage parts, because of the increasing mass of the halogenated molecules.

For the thermal capacity we obtain a constant contribution of 3.5 R for translation and rotation, which is distributed over the 5 atoms of the molecules with 0.7 R. For the vibration, increasing values of 0.2 - 0.36 R remain, with which the values of the atomic thermal capacity shown in the diagram result.
The different chemical bonds found in the examples of the above diagram allow an interpretation of these small differences in thermal capacities. Because of the decreasing electronegativity difference of the halogen-carbon bond, these bonds are weaker in polarity as the period increases. Thus the restoring forces are lower and the associated levels are closer together. The vibration frequency of the C - I bond is low, and here, at standard temperature, significantly more levels are occupied rather than for the C - F bond. This has a weak but measurable effect on the thermal capacity. The atomic entropy values increase more strongly from period to period because the force and mass effect in all three storages act in the same direction: the forces become smaller, the masses become larger.

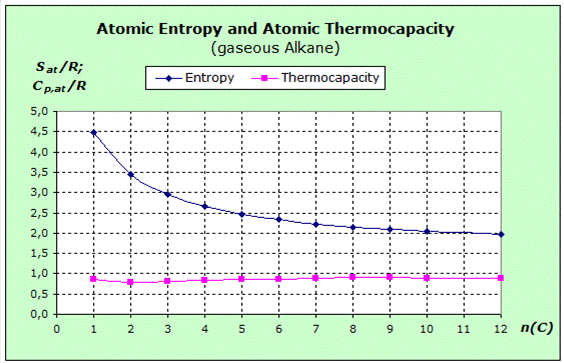
First, we notice the marked decrease in entropy as the chain length of the alkanes increases. Since all substances are gaseous, the same average volume is available for each molecule. However, since the molecules contain more atoms as the chain length increases, there is on average less space left for the single atom. The intrinsic volume of the molecules is subtracted from the total space and the remaining space is distributed to increasingly more atoms. The atoms are confined to a smaller space. According to the force rule the entropy or, more precisely, the mean entropy per atom is reduced.

Thermocapacity is obviously constant throughout the homologous series. Since all substances are gaseous, we again expect the constant contribution to the thermal capacity of 3.5 R from translation and rotation. However, this impact is distributed to more and more atoms within the homologous series, and the influence on the atomic values is lower. Since the values - as the diagram shows - are constant, somewhere replacement must come. This suggests that the compensation might come from the vibration.

The transition frequencies at the C-H and C-C bonds are very high and will hardly affect entropy and thermal capacity at room temperature. However, as the chain length increases, it becomes easier to deform this chain. Therefore, it is an interpretation that the deformation vibrations of the C-atom chains provide the contribution to the thermocapacity which leads to the constancy of these values.

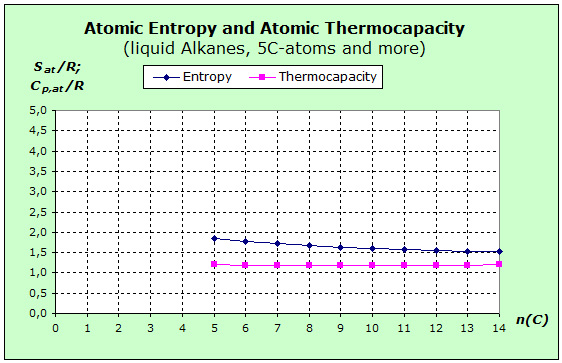
Let us now turn to the liquid organic substances. The next diagram shows the entropy and thermal capacity values of the alkanes, which are liquid at a temperature of 5 C atoms at room temperature.

It is immediately apparent that the two curves are much closer together. The entropy curve is about 0.5 R lower and the thermal capacity curve 0.4 R higher than the gaseous alkanes. Equally, however, the entropy curves are decreasing in both diagrams, while the thermal capacitances remain constant. Let us examine the question of what is different in fluids with respect to translation, rotation, and vibration than in the gas state.

From the diffusion phenomenon, we conclude that the particles in the liquid can still perform some sort of translation. However, since the free spaces are significantly smaller than in the gas state, the translation levels are further apart and lead to a lower entropy. Even if we assume the constant contribution to the thermal capacity of 2.5 R, this increase will gradually decrease with increasing chain lengthening and eventually become marginal. For already in the first substance of this series, the pentane, the base amount is distributed to 17 atoms.

Certainly, polar molecules are rotating in a liquid when building a solvation shell. However, it is not easy to say whether they rotate as freely as in the gas state. For the thermal capacity, however, we can already say that the rotation will be negligible because the constant contribution of only 1.0 R would be distributed to 17 or more atoms. For rotary entropy, it seems plausible to assume that the rotation becomes more and more difficult as the chain length increases, and that less and less rotation levels will be occupied. As a result, the decreasing rotational entropy will also make the lower values in the course of the curve understandable.

In the case of vibration, we have to take into account that, besides the covalent bonds in the molecules, van der Waals bonds between the molecules have also been added. The particles attract each other up to a certain distance, but the liquid does not collapse. Rather, there is an equilibrium with corresponding reset froces. Therefore, new vibrations occur, which must be included in the considerations. Because of the smaller amount of translation and rotation, the entropy curve is lower than that of the gaseous alkanes. The chain deformations and the transitions of the new van-der-Waals bonds provide further contributions to the course of the entropy curve. This new storage facility provides a higher thermal capacity compared with the gaseous alkanes.

After dealing with some elements, inorganic and organic substances in this chapter, we can formulate an initial summary.

• Thermal energy is mainly stored at the energy levels of translation, rotation and vibration. Electron states in the atomic shell can also store thermal energy, but under standard conditions these stores are usually not markedly filled. For this reason they are not dealt with here at first.

• In the solid state, the vibration storages are of dominant importance. The cohesion in this state depends on the chemical bonds that characterize the material and thermal properties. Force and mass rules determine not only the entropy but also the thermal energy stored up to a certain temperature. At small level intervals, ie with small resetting forces and/or large particle masses, more thermal energy is stored at the same temperature.

• In the liquid state, additional energy levels of translation and rotation are occupied and, together with the levels of the chemical bond, determine the material properties. Force and mass rules also determine the entropy of translation and rotation, but at these levels no more energy is stored with greater entropy.

• In the gaseous state, the translation and rotation storages take over the dominant importance. As the temperature increases, the vibrations are added as additional storage options.

• The monatomic gases, such as the noble gases, play a special role. The thermal energy can only be stored in translational levels because individual atoms can not rotate or vibrate. At the same temperature, all noble gases store equal amounts of thermal energy, although the heavier gases have a greater entropy.